Quote:
Originally Posted by philcski
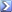
Willpays for the 5th:
1 4632 (actual odds 7-2, ML 4-1)
2 4872 (actual odds 14-1, ML 6-1)
3 19021 (actual odds 50-1, ML 20-1)
4 5951 (actual odds 3-1, ML 3-1)
5 3657 (actual odds 2-1, ML 7-2)
6 9491 (actual odds 12-1, ML 15-1)
7 47457 (actual odds 36-1, ML 20-1)
8 15845 (actual odds 6-1, ML 8-1)
9 11864 (actual odds 10-1, ML 6-1)
10 27196 (actual odds 34-1, ML 15-1)
On a rolling basis, the doubles:
Races 2-3 paid 139, parlay 114
Races 3-4 paid 239, parlay 148
Races 4-5 paid 527, parlay 408
- so right in line with what one would expect (and even a bit higher on races 3-4).
|
I don't want you to think I ignored this....
The parlay of the the 2nd through the 4th was roughly $1700 ( $1696 but we can round to make it easier ) so using the exact odds you listed here are the parlays versus the payoffs...
1 - $7650 ( payoff was 60% of parlay )
2 - $25,500 ( 19% )
3 - $85K ( 22% )
4 - $ 6800 ( 87% )
5 - $5100 ( 72% )
6 - $22100 ( 43% )
7 - $62,900 ( 75% )
8 - $11,900 ( 133% )
9 - $18,700 ( 63% )
10 - $59,500 ( 46% )
So, only the payoff on the 8 horse was better than the parlay, with all the others some version of relatively to significantly short of the parlay. Here are the amount of dollars on each potentiall winning combo...
1 - $41
2 - $39
3 - $10
4 - $32
5 - $52
6 - $20
7 - $4
8 - $12
9 - $16
10 - $7
It doesn't appear the winner ( #6 ) had a significantly lower payoff relative to the others. The average payoff was 56% of the parlay ( related to the factors I think we agreed on ) so the winning combination was hardly a statistical aberration at 43% of the parlay. The winning dollar amounts on each combination was also so small that it seems fairly easy to see how volitile the payoffs are and thus a small confluence of events will easily lead to the appearance of " low " payouts.